RatingsArticle Archive |
What is the Bayesian Resume Rating?The goal of the Bayesian Resume Rating (BRR) is to rate teams based only on wins, losses, and strength of schedule in an entirely objective manner. There are many other formulas that attempt to do the same thing, but they either use arbitrary weighting factors (e.g. RPI) or they are not mathematically sound (e.g. Colley Matrix). The specific shortcomings of other rating systems are detailed in another article.
The scope of the BRR does not include margin of victory, venue, or other extra variables. There are two reasons for this. The first is that, when evaluating a team’s body of work in the context of what it has earned (as opposed to trying to measure how good a team is), the only thing that matters in sports is whether you win or lose. Margin of victory and other factors are just style points. The second reason is that the process of accounting for those other variables is inherently subjective. The only way to account for them is to measure what their impact has been historically, and assume the impact will be similar in the future. The way that the historical impact is measured is a subjective decision, and the assumption that the impact will be similar in the future is not necessarily true. The data may be noisy, the trend may be over-fit, trends in the league may be evolving, and the amount of historical data used is a subjective choice. Some rating systems still do a very good job of overcoming these issues, and make very reliable predictions. Subjectivity isn’t inherently wrong, and those other systems aren’t bad, they just have a different scope. The BRR doesn’t use historical data from previous seasons because that would introduce bias. Each season is evaluated independent of all others, and there are no subjectively chosen constants as there are in the RPI formula. The BRR only makes two assumptions: the first assumption is that the talent levels within a league form a bell curve (normally distributed). Most teams are average, and teams gradually thin out above and below average. Due to having fewer teams, the NFL makes the best illustration: Of course, in a single competition, upsets do happen sometimes. The team that’s inherently better doesn’t win 100% of the time because all teams have days where they play better or worse than their typical performance. The second assumption in the model accounts for this. Within a given competition, a team’s standard performance can fluctuate up or down, again in a bell-curve shaped manner.
In the above example, New York is inherently better than Washington. However, the overlap in their curves illustrates that if New York has a bad day, and Washington has a good day, Washington can pull off the upset. From those two assumptions, all formulas are dictated strictly by mathematical principles. The result is that this method rates teams in a completely objective manner, accounting for a team’s entire resume, and it does so better than RPI.
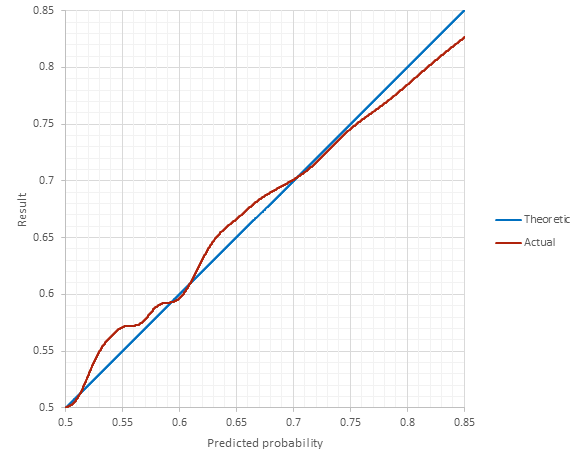
The argument can be made that these two assumptions may not be true, which is certainly a valid argument. Nonetheless, these are logical and fair assumptions, and evidence exists that they are valid. Criticisms regarding the BRR’s ability to out-perform betting-line predictions are outside the scope of the BRR. Its objective is to rate performance based on wins and losses, not to beat oddsmakers. Being that the BRR is not calibrated with historical data, validation of the theory can be shown using history. And history backs it up: The agreement seen in the historical results supports (but of course doesn't prove) the mathematical theory behind it (the real proof is the math itself). No calibration from historical data was needed to achieve this level of agreement. When it comes to rating teams based strictly on who they’ve beaten, the BRR correctly uses fundamental mathematical principals to arrive at a completely objective and proven result.
|
|