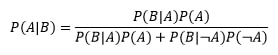Ratings

  College Football

  College Basketball

  NFL Football

Article Archive

The Relationship Between Bayes' Theorem and P-Values

This is an example of how something can be both statistically significant and unlikely to be true, using real-life data. Sometimes an explanation for a mathematical concept will just “click” for some people in ways that other explanations don’t. My hope is that this example will help people gain a more intuitive understanding of how the p-values in Null Hypothesis Significance Testing (NHST) relate to Bayes' Theorem. I’m using basketball in this example, because data is relatively easy to come by.

Let’s imagine that an NBA player got at least 15 rebounds yesterday. Knowing nothing else about the player, you might say to yourself, “15 rebounds is tough to do, and tall players have an advantage when rebounding. I bet the player who achieved that is at least 7 feet tall.”
​
Wilt Chamberlain, who stood 7’1”, has the NBA record for most career rebounds (23,924), most rebounds in a season (2149), and most rebounds in a single game (55).
Let’s analyze this statistically. We’ll start with Null Hypothesis Significance Testing. We want to calculate the p-value, which is defined as the likelihood of seeing the observed result (or more extreme than the observed result) by chance, assuming the null hypothesis is true. In our case, our hypothesis is that the player is at least 7 feet. So our null hypothesis is that he is shorter than 7 feet. One back-of-the-envelope way to calculate our p-value is simply to look at historical results. I’m going to look at NBA data from the 2018-2019 regular season (counting performances where a player logged at least 15 minutes), and assume that it's representative of the underlying probabilities. To be clear: there are certainly more statistically rigorous ways of calculating a p-value, where you don't have to make that assumption, but I want to keep this simple to illustrate a point.

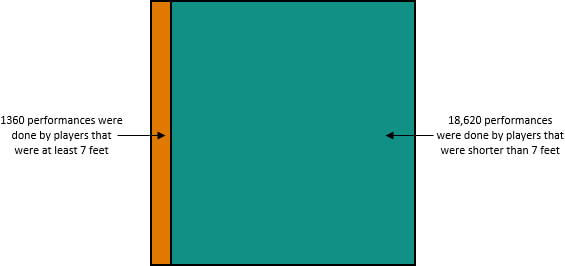
In the 2018-2019 season, there were 19,980 instances of a player logging at least 15 minutes. Focusing only on those for whom the null hypothesis is true (i.e., they are shorter than 7 feet), there were 18,620 performances. Of those 18,620 performances, 343 had at least 15 rebounds. One way to estimate the p-value is to simply take ratio of those two numbers:
​
So among the pool of 18,620 performances for whom the null hypothesis is true (the player was shorter than 7 feet), the likelihood of one of them having had at least 15 rebounds is only 1.84%. Because our p-value of 0.0184 is well below the standard cutoff for significance of 0.05, we can conclude that this performance is statistically significant.

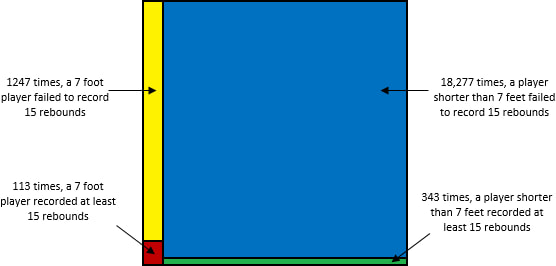
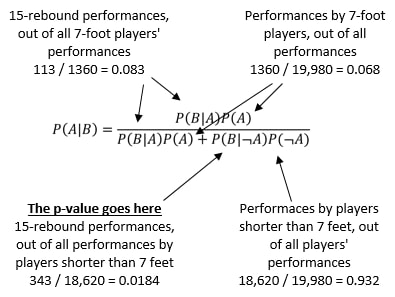
Now this is where most people get confused. They want to know what they can infer from this result. The temptation is to reject the null hypothesis, and conclude that the 15+ rebound performance was likely achieved by someone 7 feet tall or taller. However, all you can infer is this: it is unusual for a sub-7-foot player to get so many rebounds. Nothing more. Because we got a statistically significant result, we could reject the null hypothesis of the player being shorter than 7 feet, but crucially, this doesn’t imply that it’s likely the player is 7 feet or taller!

To find out how likely the player is to be at least 7 feet, we need to use Bayes' Theorem.

In Bayes' Theorem, we use P(A) to represent our prior probability (the probability of a player being at least 7 feet), and we use P(B) to represent the probability of the result we saw (the probability of a player getting at least 15 rebounds).

Over the year we’re looking at, 1360 out of the 19,980 performances were done by a player who is at least 7 feet tall. So our prior, P(A) = 1360 / 19,980 = 6.8%.
​

Among players that are shorter than 7 feet, as we already calculated, 1.84% of performances resulted in at least 15 rebounds (shown in green below). And among players that are at least 7 feet, 8.3% of performances resulted in at least 15 rebounds (shown in red below).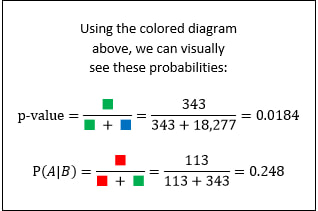
​

Now we can plug this all into Bayes' Theorem:

Picture
What our calculations show is this: Prior to knowing anything about a player, we would have guessed that a performance by a random player had a 6.8% chance of being by someone who was at least 7 feet tall. After logging 15 rebounds, the likelihood of him being at least 7 feet increased to 24.8%. An increase in confidence from 6.8% to 24.8% is good jump, but he’s still more likely than not to be shorter than 7 feet. So even though his 15+ rebound performance is statistically significant, with a p-value well below 0.05, it’s still unlikely that the player is at least 7 feet.
So why do we see such a counterintuitive result? 15+ rebounds is a rare occurrence regardless of a player’s height, so it's easy to come up with many hypotheses that will have a statistically significant null. Now, I really want to emphasize that we didn’t reject the usefulness of the p-value. It’s literally part of Bayes' Theorem. But the p-value by itself doesn’t tell the whole story.

The moral of this story is that a statistically significant p-value does not imply that the hypothesis is likely to be true. Succinctly, statistical significance does not imply likeliness. That’s why it’s critical to look beyond p-values, especially when analyzing evidence that is rare. This holds true in everything from sports to science. Bayes' Theorem gives the necessary context that’s missing from p-values alone.

I hope people find this example to be helpful in understanding the relationship between Bayes' Theorem and p-values. If you have any feedback please email me at jellyjuke@outlook.com.